| art theory 101~PIN: Pattern in Number |
|---|
from Primes to DNA
(starting with the Inverse Square Law)
© 2001, Reginald Brooks. All rights reserved.
- INTRODUCTION
- THE INVERSE SQUARE LAW (ISL)
- PRIME NUMBERS
- GEOMETRIC NUMBERS
- MAGIC SQUARES
- The diagonal sums generate the Fibonacci number sequence in the form of the Chinese Triangle. Figure. 9.
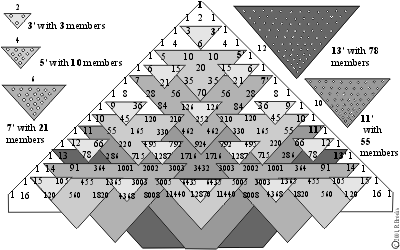
The prime numbers located within the main sequence diagonals on Pascal's Triangle reveal inverted triangular patterns symmetrically positioned within the Triangle. The basis of these inverted, triangular patterns is that they enclose sets of numbers whose members are all divisible by that prime number defining that set. For example, prime number 3 describes triangular sets whose members are all divisible by 3; prime number 5 describes triangular sets whose members are all divisible by 5; and so on. Figure. 10. In addition:
How fundamental is Nature's design esthetic. If the esthetic response to pleasing pattern designs we sentient beings experience extends all the way down to and through Nature's most fundamental levels of existence...and by that we mean way beyond leptons and quarks...to the abstract spacetime of numbers...to those very same numbers we count apples and oranges...the question...or the response...may very well be...oh! my! my! my!...or, good God!, dear Watson, what on earth were you thinking? Talk about your continuums. Surely, the Universe was never created as such for our lonely eyes to find such joy...nor is it any more likely that we were created to validate this Universe of incredible design and beauty...not to mention a seamless infinity of mystery...not likely. If Nature is number and number is Nature...in whole or part (and try to find the difference, pattern and design are the essence defining us all. The spiritual implication implied here, and by others, is not lost nor limited by journeying deeper and deeper into Nature's mystery...if anything it is greatly enhanced!
By way of introduction, a few famous, yet simple number patterns well be presented in a very brief format to lay the foundation for the remarkable patterns found in the DNA double helix. While ancient reference to many of these patterns can be found in Greek, Hebrew, Chinese and Arab cultures our references will be those found in Western sources. It should also be noted that the examination of these very simple, but profound number patterns in no way detracts from the marvelous patterning found in fractal, virtual, imaginary, irrational or complex numbering systems (for the most part). We will be dealing with simple, whole integer counting numbers...1,2,3,4,5,6,7,8,9,1O.... Irrational numbers such as p, the Golden Mean, and the Fibonacci and Padovan number series form the bridge from the patterns found in the simple whole numbers to that found in the double helix of DNA.
It should be pointed out that the patterns being referred to, in all cases, are those which have both a numerical and a visual presentation...that is the whole point.
So, before proceeding to our analysis of the remarkable patterns in DNA, we are going to take a quick sojourn through:
The Inverse Square Law (ISL) Prime Numbers Geometric Numbers Magic Squares Sequences & Proportions.
Nature's design for the cosmos can in part be distilled into fundamental laws of physics which appear to be the simplest and most immutable blueprints for the size, frequency, velocity, mass and energy of being. The Inverse Square Law (ISL), being one of those fundamental laws of physics, relates the degree or concentration of an influence (or force) to various distances of separation. Thus it is written:
| concentration | 1 | 1 | ||
| of | = | __________ | = | __________ |
| influence | distance squared | r 2 |
As the distance, r, is doubled, the influence diminishes by 1/4. When r is tripled the influence is reduced by 1/9, when r is quadrupled, the influence drops to 1/16 of the original, and so on. This is easily visualized by looking at a graphic depicting the spray of influence and its diminishing concentration (dilution) upon larger surfaces at increasing distance. Notice that a deceptively simple pattern, called the odd number summation series, develops to describe this simple geometric law. The odd numbers: 1...3...5...7... and so on, which when added to each other form the sums: 1...4...9...16…and so on. The square roots of which form the series: 1, 2, 3, 4,…and so on. See Figure 1.

Figure 1. The Odd-Number-Summation Series and the ISL
As will be shown in another work of the authors (The Geometry of Music, Art and Structure...linking Science, Art and Esthetics), this odd number summation series of the ISL has profound underpinnings not only to the well known electromagnetic and gravitational force, but to the structure of the atom itself. Indeed, it informs the diatonic scale of Western musical structure, informs the complementary relationship of the color spectrum, and has a direct connection to one of the oldest and most revered commensurate proportions of geometry, the Golden Mean. That's an awful lot to prove, so we will just take it a step at a time and try to enjoy some of the simple patterns along the way.
A prime number is any number, which can only be divided by itself, and one. By strict definition, this includes the number 1, but by convention (and most especially to satisfy the fundamental theorem in arithmetic) it is traditionally excluded.
Prime numbers become even more primal, when one realizes (Goldbach Conjecture) that every whole number greater than 1 is a sum of prime numbers.
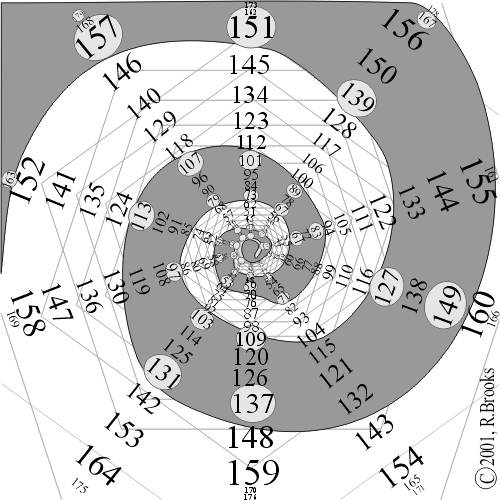
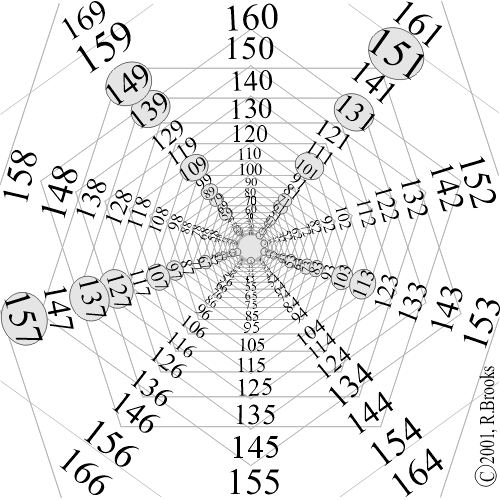
Sequentially laying out the whole numbers in geometric fashion around the pentagon reveals the following patterns (Figures 2 & 3, Table I):
-all primes above 5 end in either 1, 3, 7 or 9, and are equally distributed;
-the sums of all primes inclusive in any repeating quantity of primes sampled, are roughly equal;
-connecting the primes so arranged generates a compelling spiral image.
Figures 2. Prime Numbers Double Pentagon Spiral
Figures 3. Prime Numbers Double Pentagon Star
1 2 3 5 7 11 13 17 19 23 29 31 37 41 43
47 53 59 61 67 71 73 79 83 89 97 101 103 107 109
113 127 131 137 139 149 151 157 163 167 173 179 181 191 193
197 199 211 223 227 229 233 239 241 251 257 263 269 271 277
281 283 293 307 311 313 317 331 337 347 349 353 359 367 373
379 383 389 397 401 409 419 421 431 433 439 443 449 457 461
463 467 479 487 491 499 503 509 521 523 541 547 557 563 569
571 577 587 593 599 601 607 613 617 619 631 641 643 647 653
659 661 673 677 683 691 701 709 719 727 733 739 743 751 757
761 769 773 787 797 809 811 821 823 827 829 839 853 857 859
863 877 881 883 887 907 911 919 929 937 941 947 953 967 971
977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063
1069 1087 1091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181
1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289
1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409 1423
1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499
1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609
1613 1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723
1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861
1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933 1949 1951 1973 1979
1987 1993 1997 1999 2003 2011 2017 2027 2029 2039 2053 2063 2069 2081 2083
2087 2089 2099 2111 2113 2129 2131 2137 2141 2143 2153 2161 2179 2203 2207
2213 2221 2237 2239 2243 2251 2267 2269 2273 2281 2287 2293 2297 2309 2311
2333 2339 2341 2347 2351 2357 2371 2377 2381 2383 2389 2393 2399 2411 2417
2423 2437 2441 2447 2459 2467 2473 2477 2503 2521 2531 2539 2543 2549 2551
2557 2579 2591 2593 2609 2617 2621 2633 2647 2657 2659 2663 2671 2677 2683
2687 2689 2693 2699 2707 2711 2713 2719 2729 2731 2741 2749 2753 2767 2777
2789 2791 2797 2801 2803 2819 2833 2837 2843 2851 2857 2861 2879 2887 2897
2903 2909 2917 2927 2939 2953 2957 2963 2969 2971 2999 3001 3011 3019 3023
3037 3041 3049 3061 3067 3079 3083 3089 3109 3119 3121 3137 3163 3167 3169
3181 3187 3191 3203 3209 3217 3221 3229 3251 3253 3257 3259 3271 3299 3301
3307 3313 3319 3323 3329 3331 3343 3347 3359 3361 3371 3373 3389 3391 3407
3413 3433 3449 3457 3461 3463 3467 3469 3491 3499 3511 3517 3527 3529 3533
3539 3541 3547 3557 3559 3571 3581 3583 3593 3607 3613 3617 3623 3631 3637
3643 3659 3671 3673 3677 3691 3697 3701 3709 3719 3727 3733 3739 3761 3767
3769 3779 3793 3797 3803 3821 3823 3833 3847 3851 3853 3863 3877 3881 3889
3907 3911 3917 3919 3923 3929 3931 3943 3947 3967 3989 4001 4003 4007 4013
4019 4021 4027 4049 4051 4057 4073 4079 4091 4093 4099 4111 4127 4129 4133
4139 4153 4157 4159 4177 4201 4211 4217 4219 4229 4231 4241 4243 4253 4259
4261 4271 4273 4283 4289 4297 4327 4337 4339 4349 4357 4363 4373 4391 4397
4409 4421 4423 4441 4447 4451 4457 4463 4481 4483 4493 4507 4513 4517 4519
4523 4547 4549 4561 4567 4583 4591 4597 4603 4621 4637 4639 4643 4649 4651
4657 4663 4673 4679 4691 4703 4721 4723 4729 4733 4751 4759 4783 4787 4789
4793 4799 4801 4813 4817 4831 4861 4871 4877 4889 4903 4909 4919 4931 4933
4937 4943 4951 4957 4967 4969 4973 4987 4993 4999 5003 5009 5011 5021 5023
Table I. Prime Numbers (675)
166 primes end in 1...174 primes end in 3...169 primes end in 7...164 primes end in 9.
(Pascal's Triangle, which lies ahead, will show a truly remarkable patterned sequence of prime related numbers symmetrically, but inversely embedded within the triangle of simple whole integer numbers.)
Geometric numbers are those numbers which represent the collective quantity of points, or dots, which form simple, geometric shapes such as the triangle, square, pentagon and so on. Amazing patterns are formed by very simple rules.
Starting with nothing, add the whole numbers 1,2,3... in sequential steps to each subsequent number generated,
+1 +2 +3 +4 +5 +6 +7 +8 +9 +10...
0 1 3 6 10 15 21 28 36 45 55...
to form the triangular series;
.
. . .
. . . . . .
. . . . . . . . . .
. . . . . . . . . . . . . . . . . .
1 3 6 10 15
To form the square series, add every other number in sequential steps,
+1 +3 +5 +7 +9 +11 +13 +15...
0 1 4 9 16 25 36 49 64 ....
. . . . .
. . . . . . . . .
. . . . . . . . . . . .
. . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . .
1 4 9 16 25
To form the pentagon series, add every second number in sequential steps,
+1 +4 +7 +10 +13 +16 +19 +22...
0 1 5 12 22 35 51 70 92 ...1.
1. 2.
1. 2. 3. 4.
1. 2. 3. 4. 5.
1. 2. 3. 4. 5. 6.
1 5 12
And so on. Plotting out all these sequences reveals a connection to our next example, the Magic Squares, see Figure 4. Notice that in the tabulation of geometric number sequences, a visual geometric pattern of numbers describing the vertical / horizontal / diagonal sums of each subsequently larger Magic Square runs as the diagonal from the square number 1 on down. Above this, the row describing the triangular sequence also defines the average multipland for that respective Magic Square, i.e. the multiplands are all the numbers in that square that are evenly divided by the Magic Square number such as the average of 2 and 4 equals 3 for Magic Square 2, the average of 3, 6 and 9 equals 6 for Magic Square 3, and so on.
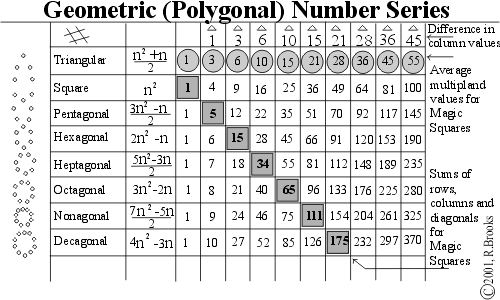
Figure 4 Geometric (Polygonal) Number Series
Magic Squares visually fill the squares whose size is determined by the Magic Square number (1,2,3,...), with one number from the consecutive numbers leading up to and including the Magic number squared in such a manner that:
All horizontal, vertical and diagonal sequences of numbers add up to exactly the same total.
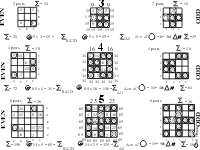
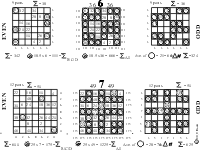
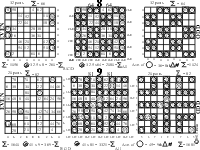
Striking visual and numerical patterns were brought out by deconstructing t he Magic Squares into odd and even components, the distribution of the multiplands (encircled numbers) and determining the characteristic number of each.
The characteristic number can be found by dividing the v/ h /d sequence sum by the Magic Square number. The characteristic number characterizes the square by determining the pattern of number distribution as related to the total sum of all the numbers. The characteristic number can be found by dividing this total sum by the square of the Magic Square number. And finally, this number can be seen to be the average value of symmetrical numbers about the center of the square. Figures 5-7.
Figure 5. Magic Squares 3-5
Figure 6. Magic Squares 6-7
Figure 7. Magic Squares 8-9
6. SEQUENCES & PROPORTIONS
Some wonderful patterns appear when simple whole integer number sequences are placed together in various simple designs. A simple one of the authors is:
| number | sums | |||||||||||||
| of | of | |||||||||||||
| row | row | |||||||||||||
| digits | digits | |||||||||||||
| ________ | __________ | |||||||||||||
| 1 | - | - | - | - | - | -> | 1 | 1=12 | ||||||
| 1 | 2 | 1 | - | - | - | - | -> | 3 | 4=22 | |||||
| 1 | 2 | 3 | 2 | 1 | - | - | - | -> | 5 | 9=32 | ||||
| 1 | 2 | 3 | 4 | 3 | 2 | 1 | - | - | -> | 7 | 16=42 | |||
| 1 | 2 | 3 | 4 | 5 | 4 | 3 | 2 | 1 | - | -> | 9 | 25=52 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | 1 | -> | 11 | 36=62 | |
| | | | | | | | | | | | | | | | | | | | | | | ... | | | ||
| ______ | _____ | _____ | _____ | _____ | _____ | _____ | _____ | _____ | _____ | _____ | | | |||
| | | | | | | | | | | | | | | | | | | | | | | | | |||
| 1 | | | | | | | | | | | | | | | | | | | 1 | reveals | |||
| 3 | | | | | | | | | | | | | | | 3 | the | |||||
| 6 | | | | | | | | | | | 6 | basic | |||||||
| 10 | | | | | | | 10 | square | |||||||||
| 15 | | | 15 | number | |||||||||||
| 21 | sequence. |
The sums of the vertical digits reveals the basic triangular number sequence.
The number of row digits recreates the odd-number-summation series.
| If you add | ||||||||
| the vertical sums | 1 | 3 | 6 | 10 | 15 | ... | ||
| to the horizontal sums | +1 | 4 | 9 | 16 | 25 | 36 | ... | revealing |
| 1 | 5 | 12 | 22 | 35 | 51 | the pentagonal number sequence. | ||
| In fact, adding | ||||||||
| the triangular | ||||||||
| number sequence | +1 | 3 | 6 | 10 | 15 | ... | ||
| generates all | 1 | 6 | 15 | 28 | 45 | 66 | ... | (the hexagonal sequence) |
| of the geometric | ||||||||
| number sequences. | ||||||||
| +1 | 3 | 6 | 10 | 15 | ... | |||
| 1 | 7 | 18 | 34 | 55 | 81 | ... | (the heptagonal sequence) | |
| ________ | ________ | ________ | ________ | ________ | ________ | ________ | ________ |
indicating that the difference between any two sequential geometric number sequences is the fundamental triangle number sequence. Also notice the appearance of the odd number summation series as seen in the ISL.
Pascal discovered (as had the ancient Chinese) that opposing two whole number sequences diagonally (which we will call the sequence diagonals) forming the sides of an equilateral triangle, generated all the numbers in between by adding the two adjacent numbers to give the number below. Encasing the outside of each sequence diagonal with 1's generated Pascal's Triangle, Figure 8.
-every number is the sum of the two adjacent numbers above, i.e. 4 + 6 = 10;
-the sum of any diagonal series of numbers is 90° below, i.e.1 + 4 + 10+20 = 35;
-the sum of all the numbers in the nth row equals2n , i.e. 1 + 2 = 4 = 22;
-the sum of all the numbers in all rows above the nth row=2n -1, i.e.23 - 1 = 7;
-the sum of all the numbers in any row is twice the sum of the previous row added;
-square any number in the diagonal sequence, subtract the number next to it inside, and the remainder number is found directly below, i.e. 42 - 6 = 10.
Pascal's Triangle
| 1 | |||||||||||||||||||||||||||||||||
| 1 | 1 | ||||||||||||||||||||||||||||||||
| 1 | 2 | 1 | |||||||||||||||||||||||||||||||
| 1 | 3 | 3 | 1 | ||||||||||||||||||||||||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||||||||||||||||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | ||||||||||||||||||||||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | |||||||||||||||||||||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | ||||||||||||||||||||||||||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | |||||||||||||||||||||||||
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | ||||||||||||||||||||||||
| 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | |||||||||||||||||||||||
| 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 | ||||||||||||||||||||||
| 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 | 12 | 1 | |||||||||||||||||||||
| 1 | 13 | 78 | 286 | 715 | 1287 | 1716 | 1716 | 1287 | 715 | 286 | 78 | 13 | 1 | ||||||||||||||||||||
Figure. 8. Pascal's Triangle
In addition, Pascal's Triangle may be used to reveal the coefficients i n the binomial expansion (a+b) n, as well as combinatorial and probability solutions.
Two other very interesting patterns emerge relating Pascal's Triangle to two other great pattern systems:
| F | I | B | O | N | A | C | C | I | S | E | R | I | E | S | ||||
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | ... | ... | ||||
| 1 | / | / | / | / | / | / | / | / | / | / | / | / | / | / | / | / | / | / |
| 1 | 1 | / | / | / | / | / | / | / | / | / | / | / | / | / | / | / | / | |
| 1 | 2 | 1 | / | / | / | / | / | / | / | / | / | / | / | / | / | / | / | / |
| 1 | 3 | 3 | 1 | / | / | / | / | / | / | / | / | / | / | / | / | / | / | / |
| 1 | 4 | 6 | 4 | 1 | / | / | / | / | / | / | / | / | / | / | / | / | / | / |
| 1 | 5 | 10 | 10 | 5 | 1 | / | / | / | / | / | / | / | / | / | / | / | / | / |
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | / | / | / | / | / | / | / | / | / | / | / | / |
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | / | / | / | / | / | / | / | / | / | / | / |
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | / | / | / | / | / | / | / | / | / | / |
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | / | / | / | / | / | / | / | / | / |
| 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | / | / | / | / | / | / | / | / |
Figure. 9. Chinese Triangle & The Fibonacci Series
The Fibonacci number series, a sequence in which each subsequent number is the sum of the two previous numbers, very nearly approaches the ideal growth proportion known by the Greeks as the Divine Proportion or the Golden Mean, f . For example, 2 1/13 = 1.615 and 34/21 = 1.619, the average being 1.617. ~= 1.618 and represents the perfectly commensurate proportion described by;
a + b = b/( a : b) = b/ ( a/b) = b 2 /a
or
a : b = b/ (a + b)
That is, the root (a) is increased to a degree (b), the sum of which (a + b) equals the inverse ratio of the root (1/ a) to its movement root squared (b2 ). In other words, the growth, or newly generated size is exactly larger (or smaller) by an amount that is strictly commensurate with both the total sum of the new and the older sizes. The Golden Mean is based on the square.
Another sequence series, the Padovan series, based on the triangle, expands its series by adding the second and third previous number, and gives a constant ratio of 1.3247. This series also generates amazing, interconnected commensurate design patterns, many of which suggest 3D applications.
-each prime number minus 1 = the number of members (numbers) forming the base of the inverted triangle;
-each prime number times 1/2 of its base number (as defined above) = the total number of members (numbers) in that triangular set.
Figure 10. Pascal's Triangle & Prime Numbers
| # of | base | Total # | ||||||||
| Prime | (minus) | (equals) | members | member # | (times) | (equals) | members | |||
| number | - | one | = | across base | divided by | x | Prime | = | in | |
| triangle | of triangle | two | number | triangle set | ||||||
| 3 | - | 1 | = | 2 | 1 | x | 3 | = | 3 | |
| 5 | - | 1 | = | 4 | 2 | x | 5 | = | 10 | |
| 7 | - | 1 | = | 6 | 3 | x | 7 | = | 21 | |
| 11 | - | 1 | = | 10 | 5 | x | 11 | = | 55 | |
| 13 | - | 1 | = | 12 | 6 | x | 13 | = | 78 | |
| 17 | - | 1 | = | 16 | 8 | x | 17 | = | 136 | |
| 19 | - | 1 | = | 18 | 9 | x | 19 | = | 171 | |
| 23 | - | 1 | = | 22 | 11 | x | 23 | = | 253 | |
| 29 | - | 1 | = | 28 | 14 | x | 29 | = | 406 | |
| 31 | - | 1 | = | 30 | 15 | x | 31 | = | 465 | |
| 37 | - | 1 | = | 36 | 18 | x | 37 | = | 666 |
Table II. Pascal's Triangle and the Prime Number Triangular Sets
The third diagonal sequence of numbers, that which lies next to the main sequence diagonal, is none other than the triangular geometric number series we covered early on. We would like to point out a very unusual and unexpected relationship, or pattern, between this sequence and that of the prime number triangular sets found in Pascal's Triangle.
First, the prime numbers, from 3 upwards, are separated from each subsequent prime by the following sequence pattern: 2, 2, 4, 2, 4, 2, 4, 6, 2, 6.….
Secondly, the total members (#) sums with each respective prime number triangular set are: 3, 10, 21, 55, 78, 136, 171, 253, 406, 465, 666,….
Thirdly, the triangular geometric number series progresses as shown on Pascal's Triangle in lockstep with the main sequence diagonal whole numbers and the prime numbers contained within, such that, for every prime number, the triangular geometric number next to it reveals the total member (#) sum for that triangular set. Thus the pattern: 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, is maintained. See Table III.
| Triangular | Sequence | Prime | Total |
| Geometric | pattern | numbers | member |
| number | separating | in | (#) |
| series | Primes | BOLD | sums |
| 1' | 0 | ||
| 1 | 2' | 0 | |
| 3 | 3' | 3 | |
| 6 | 2* | 4 | 0 |
| 10 | 5' | 10 | |
| 15 | 2 | 6 | 0 |
| 21 | 7' | 21 | |
| 28 | 8 | 0 | |
| 36 | 4 | 9 | 0 |
| 45 | 10 | 0 | |
| 55 | 11' | 55 | |
| 66 | 2 | 12 | 0 |
| 78 | 13' | 78 | |
| 91 | 14 | 0 | |
| 105 | 4 | 15 | 0 |
| 120 | 16 | 0 | |
| 136 | 17' | 136 | |
| 153 | 2 | 18 | 0 |
| 171 | 19' | 171 | |
| 190 | 20 | 0 | |
| 210 | 4 | 21 | 0 |
| 231 | 22 | 0 | |
| 253 | 23' | 253 | |
| 276 | 24 | 0 | |
| 300 | 25 | 0 | |
| 325 | 6 | 26 | 0 |
| 351 | 27 | 0 | |
| 378 | 28 | 0 | |
| 406 | 29' | 406 | |
| 435 | 2 | 30 | 0 |
| 465 | 31' | 465 | |
| 496 | 32 | 0 | |
| 528 | 6 | 33 | 0 |
| 561 | 34 | 0 | |
| 595 | 35 | 0 | |
| 630 | 36 | 0 | |
| 666 | 37' | 666 |
Table III. The Triangular Geometric Numbers and the Prime Numbers as indicators of the Prime Number Triangular Sets in Pascal's Triangle. The *2,2,4,2,4,2,4,6,2,6 pattern of difference between both prime numbers and triangular geometric numbers which match.
This concludes our look at historical number patterns. Let us now proceed to see what sort of tricks Nature has in store for us in that most geometric, yet enigmatic molecule of life; the DNA double helix.
7. NUMBER PATTERNS IN DNA
[This part of the paper has been extracted out, updated and adapted to the web under a separate title: GoDNA: The Geometry of DNA (axial view),
in order to give this marvelous, magical molecule of Nature its own proper due. Please visit the link above and return to this same spot by the link back (or use your "back" button).]8. STRUCTURE & CHEMISTRY OF DNA
[ As noted above, the main section of the Number Patterns in DNA has been given its own title, GoDNA: The Geometry of DNA , and a separate section to go to view this work. This section, has also been extracted from Patterns In Number (PIN), reworked and adapted for the web as: SCoDNA: The Structure & Chemistry of DNA (axial view). It builds on the foundation laid down in GoDNA. It is for those who wish to get deep into the design (and chemistry) of the DNA double helix as presented in the composite axial view. Others may want to skip this section altogether but I do hope you will peruse GoDNA to see first hand the marvelous number magic and pattern. For those who are digging in, you will need to access GoDNA and the Figures and Tables contained within, to proceed from here.]
9. CONCLUSION
For some, the debate over the nature of Nature is always one of polemics... order versus chaos.... determinate versus indeterminate.. evolution versus divine intervention... temporal versus spatial.. .or, fundamentally, wave versus particle.
If there is anything that the last century has taught us it should include this: The apparent dualism of all that we know of Nature, which includes, but should not be limited by, our anthropic vision, is really a multidimensional construct in which individual continuums such as space and time, wave and particle, order and chaos, and, determinism and indeterminism (to name a few), are not polemical sets, but instead actually are individual continuums whose dynamic is released when placed perpendicularly at right or other angles to each other. This interactional dynamic is formed in and of the multidimensional construct of such continuums crossing. Think dimensional.
10. REFERENCES
This work is based on simple concepts on elementary geometry, driven by a love for pattern seen in numbers, as in Nature. The simplicity defies the diversity, yet it is through a combination of fixed, almost rigid and constant symmetry with limited, asymmetric variables that the fabric of life is woven. From the original computer generated imagery of DNA by the pioneering Robert Langridge (http://www.cgl.ucsf.edu/home/rl/index.html) over 20 years ago, I analyzed and subsequently deconstructed the image pattern into a number of geometric forms, the primary ones being a series of concentric double pentagons. In 1995 I rebuilt the pattern on the surface of a large sculpture ("Out of Africa, from mime to five, DNA").That same year I had started an ambitious paper: "The Geometry of Music, Art and Structure...linking Science, Art and Esthetics". Revised in 1996 and further revised and condensed in the final published version in 1998. My work on the Geometry of DNA was a small part of this work. I more fully developed GoDNA in the next interim work: "Pattern in Number...from Primes to DNA" in 1997, and have since readied it for formal publication in Part 2 of "The Geometry of Music, Art and Structure...linking Science, Art and Esthetics". The ideas presented in the white papers were part of my gallery shows at the former Montage Gallery in Portland, Oregon in the mid 1990's.
"The Geometry of Music, Art and Structure...linking the esthetics of Art and Science", Part 1, was
presented at the 8th ICECGDG (International Conference on Engineering Design Graphics and Descriptive
Geometry, sponsored by the International Society for Geometry and Graphics, the Japan Society for
Graphic Science, and the Engineering Design Graphics Division of the American Society for Engineering
Education; hosted by the College of Engineering, The University of Texas at Austin (1998). Published
in the Proceedings of the 8th ICECGDG, Vol. 2, pg 378, ISGG, Tokyo, Japan, 1998.
Other text references:
1. Clawson, Calvin C., Mathematical mysteries: The Beauty and Magic of Numbers Plenum Press, New York, NY, 1996
2. Huntley, H. E., The Divine Proportion: A Study in Mathematical Beauty, Dover Publications, New York, NY, 1970
3. King, John, The Modern Numerology, Blandford Publications, U.K., 1996
4. Ribenboim, Paulo, The Book of Prime Number Records, Springer-Verlag, New York, NY, 1988
5. Vajda, S., Fibonacci and Lucas Numbers, and the Golden Section: Theory and Application, Ellis Horwood Limited, West Sussex, England, 1989
Links:
These links to further resources, while not used in this paper as references, nevertheless provide a great deal more depth to those themes leading up to the Geometry, Structure and Chemistry of DNA.
Caldwell, Chris, The Prime Pages
Leatherland, Adrian J.F.,Pulchritudinous Primes
Watkins, Matthew R., Number Theory & Physics Archive
number 7, Aesthetics of the Prime Sequence
???, Prime Number Spiral
Heinz, Harvey, Primes
Rivera, Carlos, Prime Puzzles
Weisstein. Eric, Eric Weisstein's World of Mathematics, Pascal's Triangle
Bogomolny, Alexander, Interactive Mathematics Miscellany and Puzzles
???, The Math Forum
???, Pascal's Triangle And Its Patterns
Suzuki, Mutsumi, Magic Squares
Heinz, Harvey, Magic Squares, Magic Stars & Other Patterns
Kelly, Charlie, Magic Squares and Hyper Cubes
Weisstein, Eric, Eric Weisstein,s World of Mathematics-Magic Squares
Danielsson, Holger, Magic Squares
Copyright© 2001-06 Reginald Brooks, BROOKS DESIGN. All Rights Reserved.
click to go to Special Graphics Section: digital 2D works: GoDNA
click to go to new paper on primes, Part 1: "Butterfly Primes"
click to go to new paper on primes, Part 2: "The Butterfly Prime Directive"
click to go to new media net.art work "Butterfly Primes ... Prejudicial Numbers"